Regression Analysis
Regression analysis is a fundamental technique in predictive modeling that aims to understand the relationship between a dependent variable and one or more independent variables. There are two primary types of regression: linear regression and logistic regression.
Linear Regression
Linear regression assumes a linear relationship between the dependent variable (often denoted as Y) and the independent variables (denoted as X). The goal is to find the best-fitting line that minimizes the sum of squared errors between the predicted and actual values.
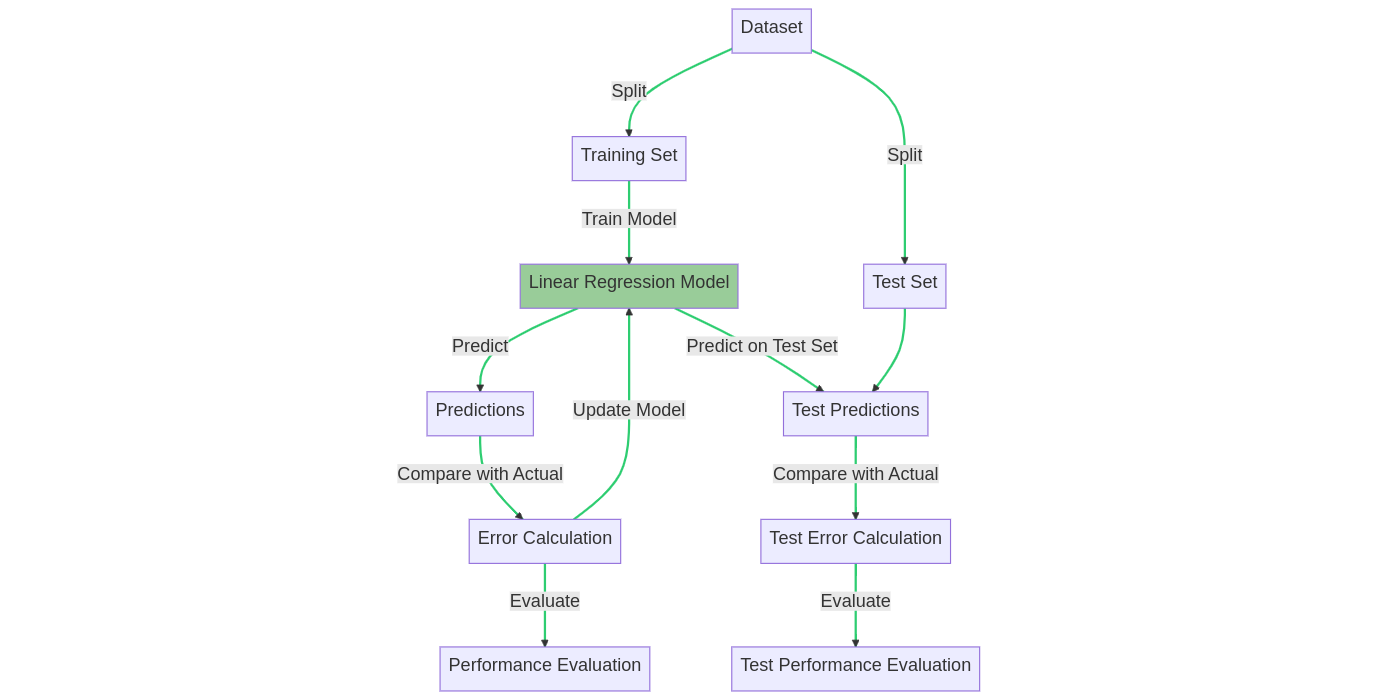
Linear regression model training and prediction processes
Logistic Regression
Logistic regression, on the other hand, deals with binary outcomes (e.g., success or failure). It models the probability of an event occurring as a function of the independent variables. Logistic regression is particularly useful for classification problems.
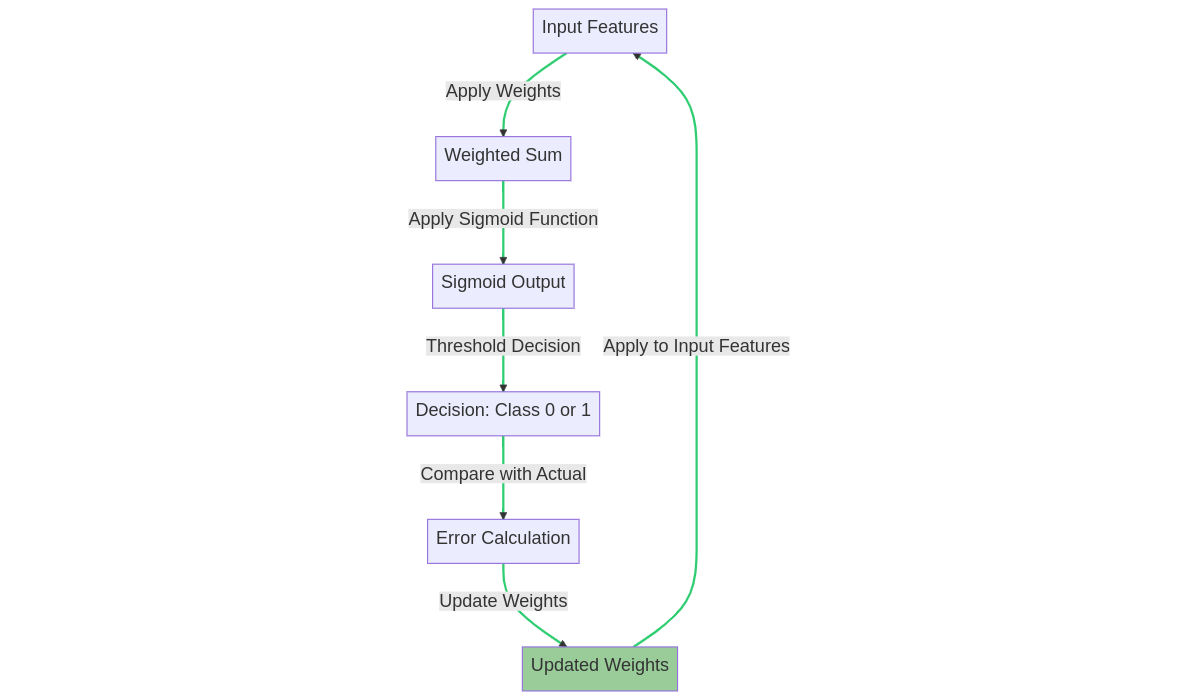
Logistic regression weights updating process
Decision Trees
Decision trees are another popular technique for predictive modeling. They work by recursively splitting the data into subsets based on the values of the input features, ultimately leading to leaf nodes that represent a decision or prediction.
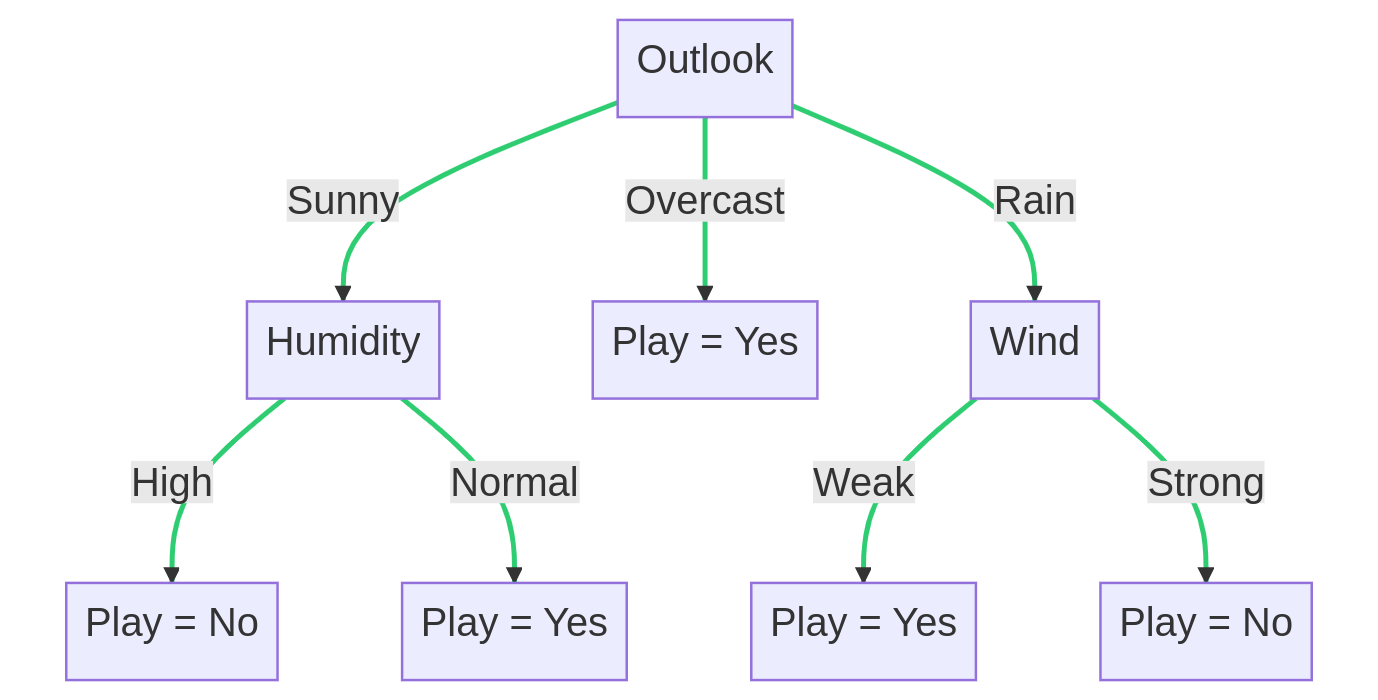
An example decision tree diagram
- Advantages: Decision trees are easy to understand and interpret, and they can handle both numerical and categorical data.
- Disadvantages: They are prone to overfitting, which occurs when the model becomes too complex and captures noise in the data.
Ensemble Methods
Ensemble methods combine multiple models to improve the overall performance of the predictive model. Two popular ensemble methods are bagging and boosting.
Bagging
Bagging, or bootstrap aggregating, involves training multiple models on different subsets of the data (with replacement) and averaging their predictions. Bagging can help reduce overfitting and improve the stability of the model.
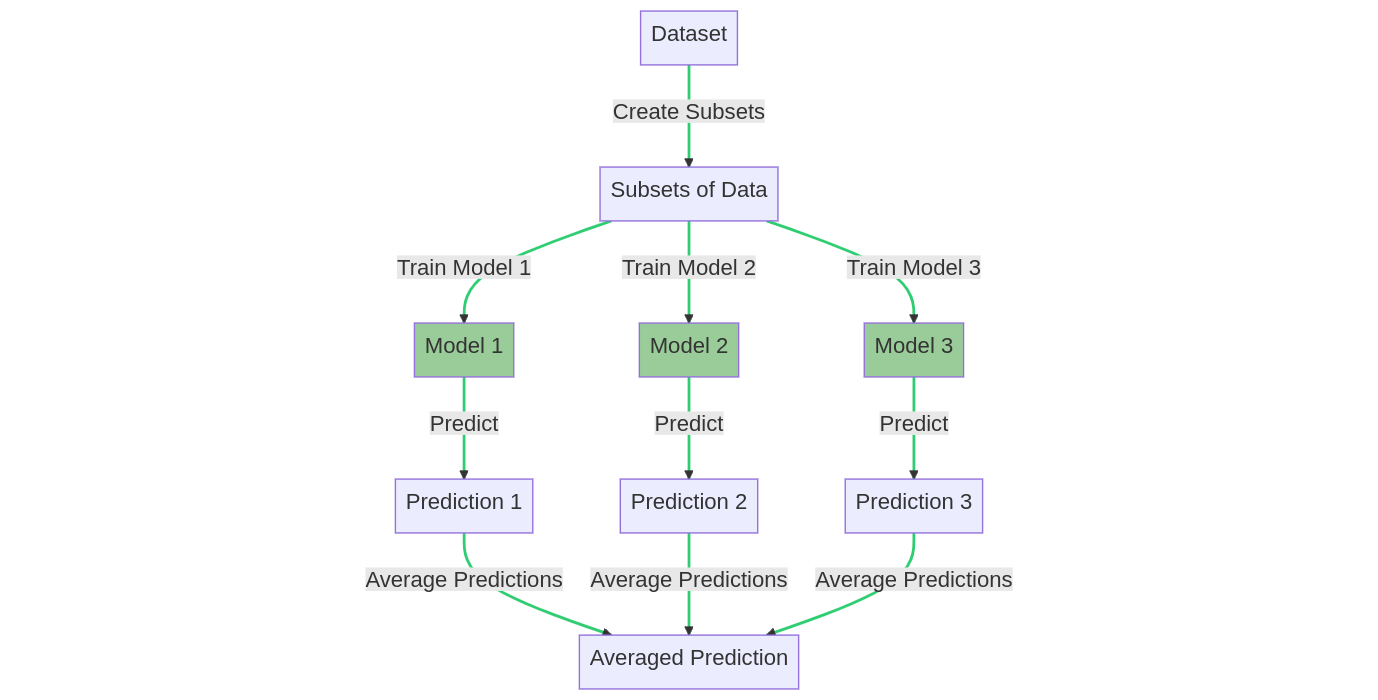
The bagging training process
Boosting
Boosting is another ensemble method that aims to build a strong model by combining a series of weak models. Each new model is trained to correct the errors made by the previous model, thus improving the overall performance.
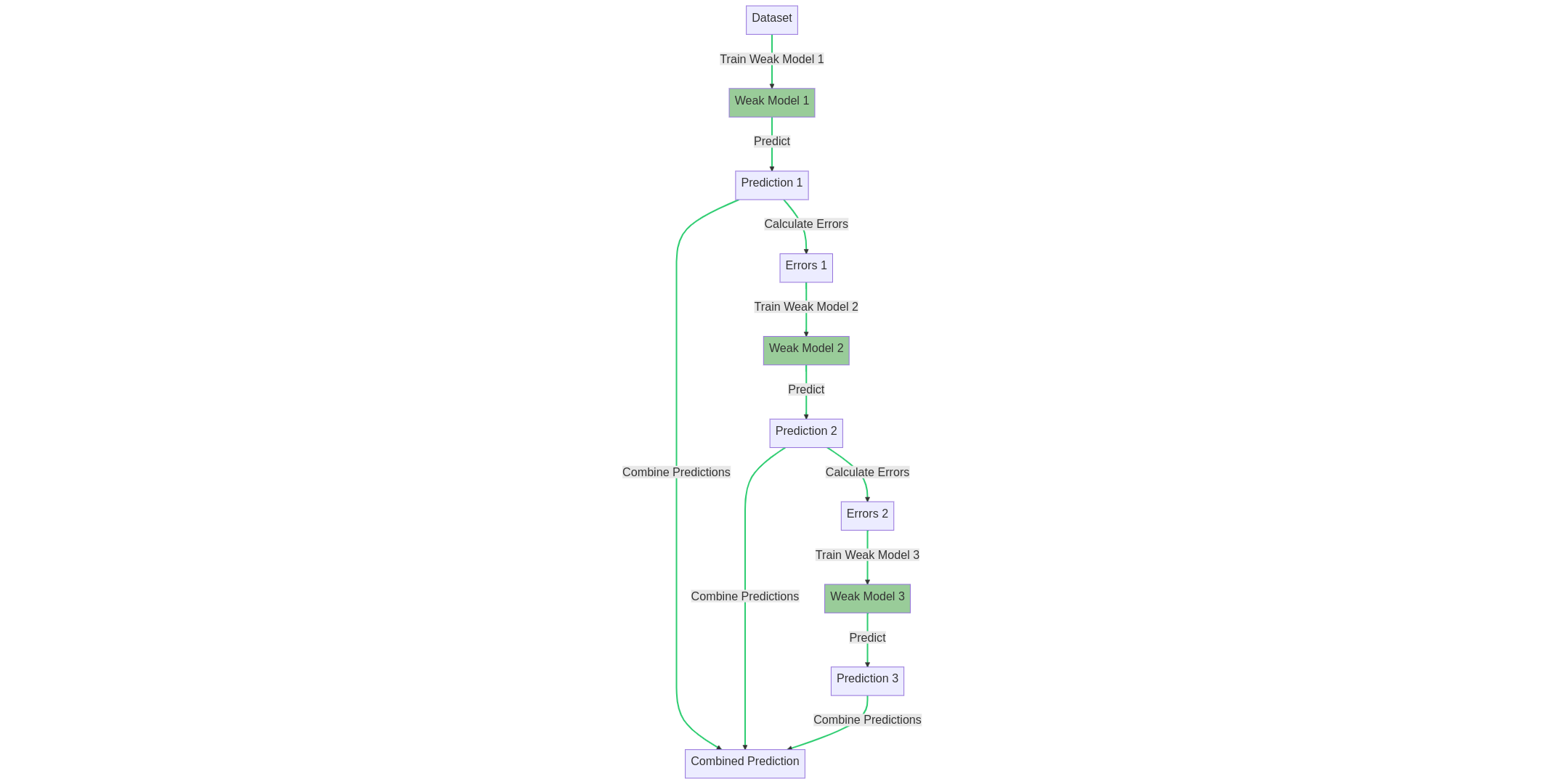
The boosting training process
Random Forests
Random forests are an extension of the bagging technique applied to decision trees. In random forests, each tree is trained on a random subset of the data and a random subset of the features. The final prediction is obtained by averaging the predictions of all the trees.
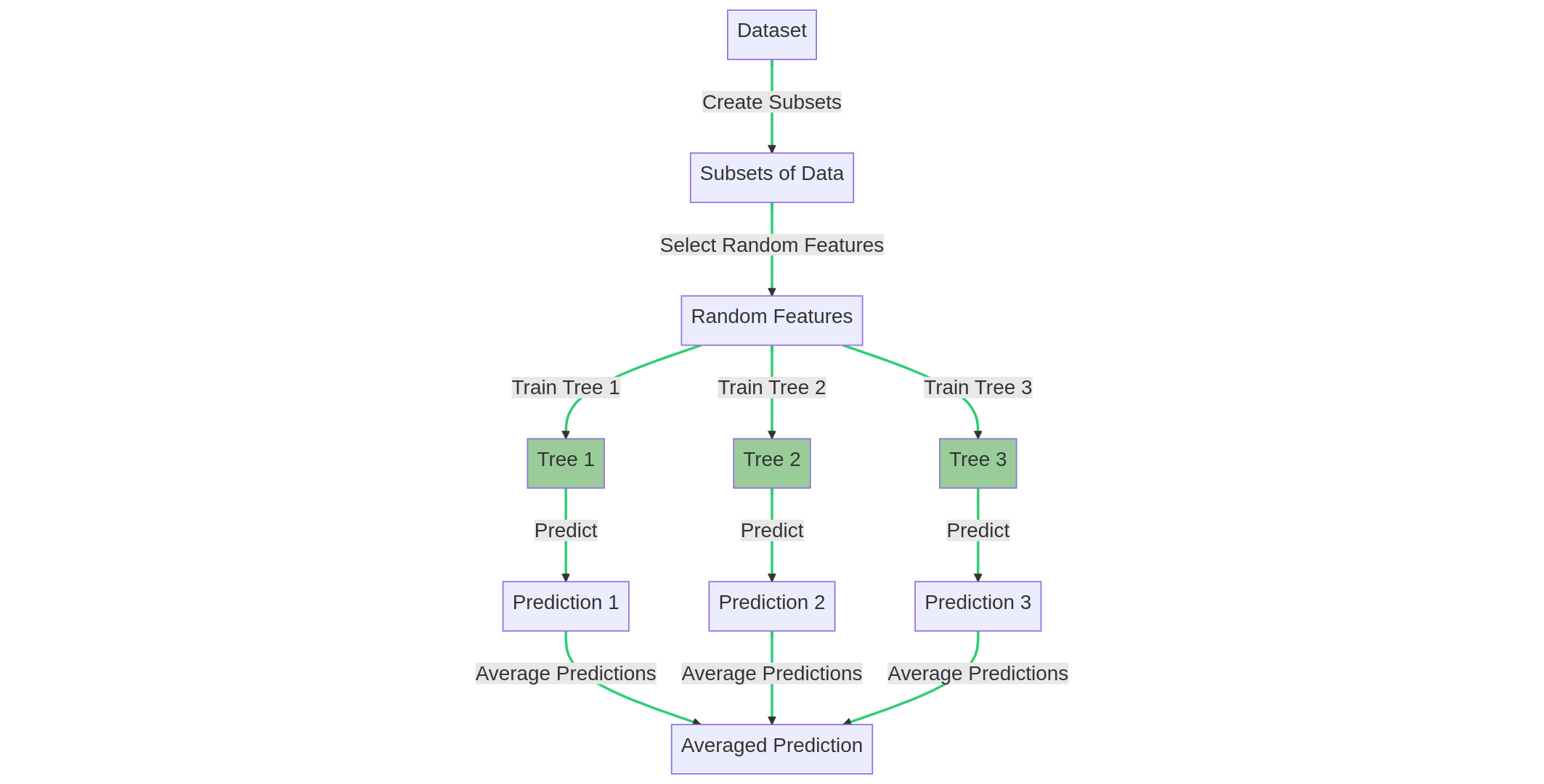
The random forest training process
- Advantages: Random forests are highly accurate, robust to noise and outliers, and can handle large datasets with many features.
- Disadvantages: They can be computationally expensive and harder to interpret than single decision trees.
A Final Word
In conclusion, predictive modeling is a powerful tool that can help us make informed decisions based on historical data. By understanding the strengths and weaknesses of different techniques, from regression to random forests, we can choose the appropriate method for our specific problem and build a more accurate and reliable model.
| Technique | Description | Advantages | Disadvantages |
|---|---|---|---|
| Linear Regression | Aims to understand the linear relationship between a dependent variable and one or more independent variables | • Provides a simple and interpretable model • Suitable for continuous dependent variables |
• Assumes a linear relationship, which may not be appropriate in all cases • Prone to outliers |
| Logistic Regression | Deals with binary outcomes and models the probability of an event occurring based on independent variables | • Useful for classification problems • Provides interpretable coefficients indicating feature importance |
• Assumes a linear relationship between the log-odds and independent variables • Requires large sample sizes for stable estimates |
| Decision Trees | Split the data into subsets based on input features to make decisions or predictions | • Easy to understand and interpret • Handles both numerical and categorical data |
• Prone to overfitting and capturing noise in the data • May result in complex trees |
| Bagging | Trains multiple models on different subsets of data and averages their predictions | • Reduces overfitting • Improves model stability |
• May require more computational resources • Sacrifices interpretability |
| Boosting | Builds a strong model by sequentially correcting errors made by weak models | • Improves overall performance • Handles complex relationships between variables |
• Sensitive to noisy data • May be computationally expensive |
| Random Forests | Ensemble of decision trees trained on random subsets of data and features, with predictions averaged | • Highly accurate and robust • Handles large datasets with many features |
• Can be computationally expensive • Harder to interpret compared to single decision trees |





