As machine learning practitioners, one critical aspect we often grapple with is tuning the hyperparameters of our models. A delicate balance of these hyperparameters is essential to maximize the performance of our machine learning models, and this is where hyperparameter tuning methods, such as Grid Search and Random Search, come into play.
In this article, we will shed light on these two popular techniques, explaining their inner workings, comparing their advantages and limitations, and showcasing their application through Python code snippets. By the end of this guide, you will be able to determine when to use each method, thus enhancing your model’s performance in various scenarios.
Understanding Grid Search
Grid Search, also known as an exhaustive search, is a traditional method that is used when dealing with a manageable number of hyperparameters. It functions by systematically working through multiple combinations of parameter tunes, cross-validate each and determine which one gives the best performance. Essentially, you define a grid of hyperparameters and it will try out every possible combination in order to determine the optimal values.
Given its exhaustive nature, Grid Search can be highly computationally expensive, particularly when dealing with a large number of different hyperparameters and much bigger datasets. This can lead to longer training times and, in some cases, overfitting of the model on the training set. However, despite these limitations, it guarantees that the best combination is reached if the optimal solution lies within the grid.
from sklearn.model_selection import GridSearchCV
# Defining the hyperparameters
param_grid = {'C': [0.1, 1, 10, 100], 'gamma': [1, 0.1, 0.01, 0.001], 'kernel': ['rbf']}
grid = GridSearchCV(SVC(), param_grid, refit=True, verbose=2)
grid.fit(X_train, y_train)
Here, GridSearchCV from sklearn library is used for tuning parameters of the Support Vector Classifier (SVC).
Understanding Random Search
Random Search is a practical, stochastic method used for hyperparameter optimization. Instead of exploring the whole parameter space, it samples a random set of parameters and evaluates their performance. The underlying theory here is that, not every hyperparameter is as important, and random search allows for a more diverse set of parameters to be evaluated.
Random Search can be highly beneficial when there are less critical hyperparameters, which is often the case. Unlike Grid Search, it does not suffer from the curse of dimensionality. However, it’s worth noting that since Random Search is stochastic in nature, the result might not be the same every time the algorithm is run. The trade-off between speed and optimality in Random Search makes it an excellent choice when time is a constraint.
from sklearn.model_selection import RandomizedSearchCV
# Defining the hyperparameters
param_dist = {'C': [0.1, 1, 10, 100], 'gamma': [1, 0.1, 0.01, 0.001], 'kernel': ['rbf']}
rand = RandomizedSearchCV(SVC(), param_dist, refit=True, verbose=2)
rand.fit(X_train, y_train)
The RandomizedSearchCV function is utilized here to tune parameters for the SVC model, akin to the previous example.
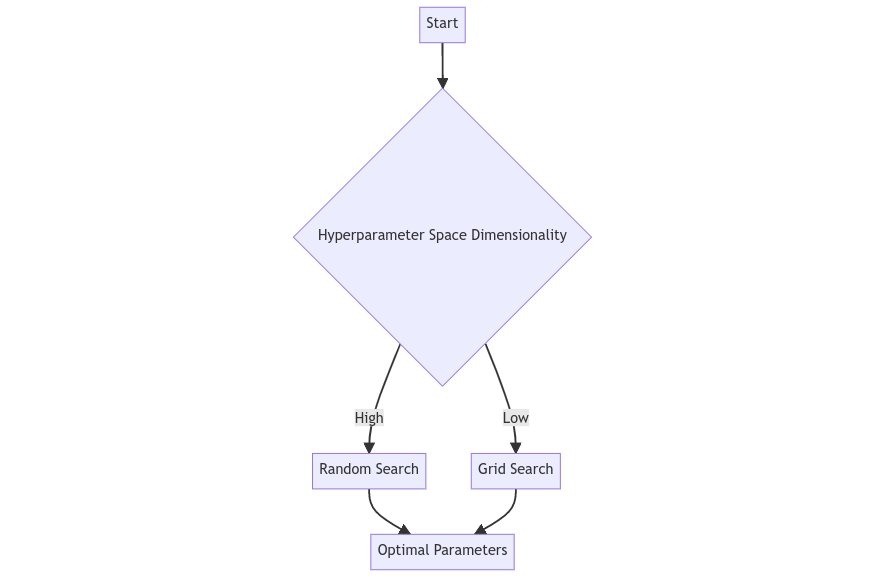
Grid Search vs Random Search
While Grid Search guarantees the best subset of hyperparameters from the specified list, it can be computationally expensive. On the other hand, Random Search may not always provide the most optimal results but is usually faster and more efficient, particularly in scenarios where the dimensionality of the hyperparameter space is high.
Conclusion
Choosing between Grid Search and Random Search can be a matter of trade-off based on your specific needs and constraints. While Grid Search can ensure the optimal solution, Random Search can provide a near-optimal solution much faster, which can be crucial in many real-world applications.
Mastering these techniques is a significant step towards becoming an effective machine learning practitioner. We hope that this guide has demystified these two methods, empowered you to make an informed choice, and enabled you to fine-tune your models more effectively.





